Scarlet fever (SF) is a common communicable disease that results from group A Streptococcus (GAS) infections^[1]. SF accounted for the global loss of life among children 5–15 years of age in the 18th and 19th centuries^[2]. A rapid reduction in SF morbidity and mortality occurred due to the scale-up of effective antibiotics and improvements in sanitation and nutrition^[3]. The unexpected increase in the incidence of SF has attracted a renewed interest in infectious diseases^[3]. Because the triggers that cause SF outbreaks are not fully understood and there is a scarcity of available vaccines protecting susceptible populations from GAS infections, effective prevention and control plans are required to stop the continued spread of SF.

Time series analysis assists in the development of hypotheses to explain the temporal patterns of different diseases and to analyze the spread, therefore, facilitating the creation of a quality forecasting system. The seasonal autoregressive integrated moving average (SARIMA) model has been widely applied to estimate the epidemiological patterns of contagious diseases because this model has a simple structure, fast applicability, and a relatively high forecasting reliability level ^[4]. It has been shown that the SARIMA model is able to satisfactorily estimate a simple time series ^[4], but it is difficult to manage complex time series, such as the data with multiple seasonal periods, high-frequency seasonality, non-integer seasonality, and dual-calendar effects. By comparison, the innovation state-space modelling framework that combines Box-Cox transformations, Fourier series with time-varying coefficients, and autoregressive moving average (ARMA) error correction (known as the TBATS method) is customized for use with the patterns included in a complex time series described above ^[5]. In addition, the TBATS model is used for linearity and some types of non-linearity in a complex time series based on Box-Cox transformations ^[5], which makes it possible to perform a multistep ahead prediction. Moreover, the TBATS model is able to decompose a complex seasonal time series into its trend, seasonal, and irregular components ^[5], which is not able to be undertaken by use of the SARIMA model. Importantly, SF morbidity has been shown to display dual seasonal patterns in some countries. Therefore, this study analyzed the long-term epidemic patterns using the TBATS model. The forecasting power under the TBATS model was compared with the SARIMA model.

We obtained the monthly SF incidence and population data between January 2004 and December 2019 from the Chinese CDC and the Statistical Yearbook of China, respectively. Then, we partitioned the SF morbidity series into two segments comprising a training dataset from January 2004 to December 2017 to construct the SARIMA and TBATS models and a testing dataset from January 2018 to December 2019 to test the generalization of both models. Two additional datasets were provided to test the robustness of both models: the first 180 data sets from January 2004 to December 2018 and 156 data sets from January 2004 to December 2016 were treated as training datasets, respectively; and the remainder were testing datasets. We estimated the changing epidemiologic trends of SF based on annual percentage change (APC) and average APC (AAPC) using the Joinpoint regression program (version 4.8.0.1). We constructed the TBATS model with the “forecast,” “tseries,”, and “FinTS” packages in R software (version 3.4.3). The incidence rate ratio (IRR) with a 95% uncertainty limit (UL) before and after the SF outbreak was calculated using the method proposed by Armitage and Berry ^[6]. The mean absolute deviation (MAD), root mean square error (RMSE), mean absolute percentage error (MAPE), mean error rate (MER), and root mean square percentage error (RMSPE) were computed to compare the forecasting ability of both models.

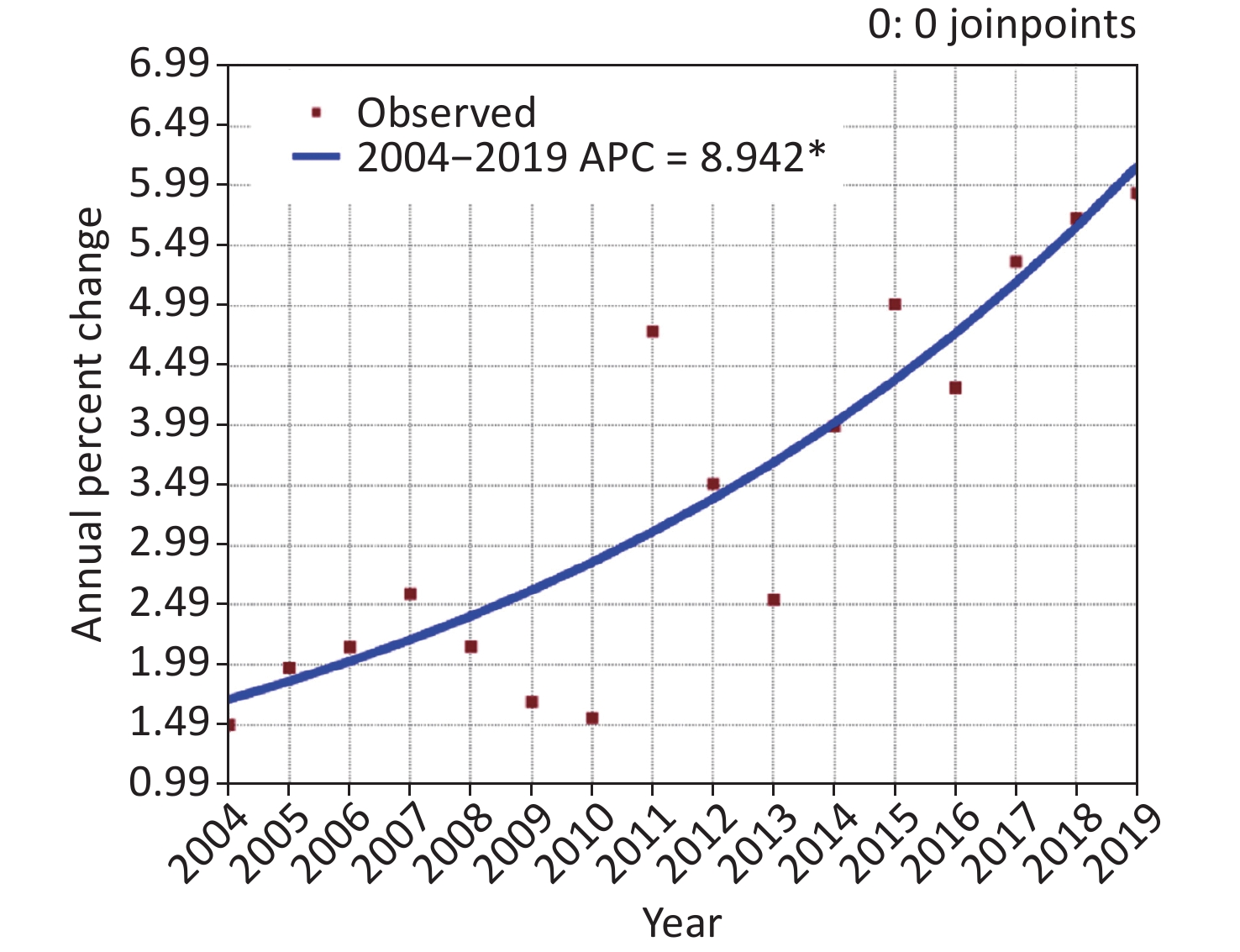
During the study period, a notable increase in SF morbidity was detected, with an AAPC = 8.942 (95% UL: 5.995–11.971; t = 6.697, P < 0.001; Supplementary Figure S1, available in www.besjournal.com), and the highest morbidity (5.930/100,000 persons) occurred in 2019, which increased by a factor of nearly four compared with the lowest level (1.489/100,000 population) in 2004 (Supplementary Figure S2, available in www.besjournal.com). The SF epidemics remained relatively steady from 2004–2010 (average, 1.937/100,000 persons annually), with an AAPC = −0.840 (95% UL: −7.678 to 6.505; t = −0.231, P = 0.817). An unexpected outbreak was witnessed in 2011, and since then a rapidly increasing trend occurred (average, 4.580/100,000 persons annually [excluding 2013]; the exact causes regarding this annual drop are unknown; Supplementary Figure S2), with an AAPC = 5.952 (95% UL: 0.239–11.992; t = 2.466, P = 0.043), which showed good agreement with a resurgence of SF in Hong Kong, China^[7], but inconsistent with England where the resurgence occurred in 2014 ^[8]. There has been a doubling in the SF incidence during the post-resurgence periods compared with the pre-resurgence periods (IRR = 2.364, 95% UL: 2.358–2.370). Nevertheless, the driving force associated with the increased pathogenicity of GAS fails to be elucidated. A possible explanation may be due to the acquisition of novel prophages harboring new hybridizations of toxin genes and antimicrobial resistance genes, which is related to the emergence and expansion of the predominant genotypes of emm12 and emm1 in China ^[3]. Another explanation may be associated with the natural periodicity of the SF incidence (SF epidemics are characterized by a cyclic change of approximately 6 years ^[3]). A third explanation may be linked to the relaxation of the 2-child policy in 2011 ^[3], which led to an increase in the number of susceptible individuals. A fourth reason may be attributed to improvements in the diagnostic capacity and the increased awareness of medical workers in reporting SF ^[3]. A fifth reason may be a result of the deterioration of air quality in China ^[9], despite the gradual improvements in the last 2 years. Finally, there are no vaccines available to prevent infections with GAS until now.

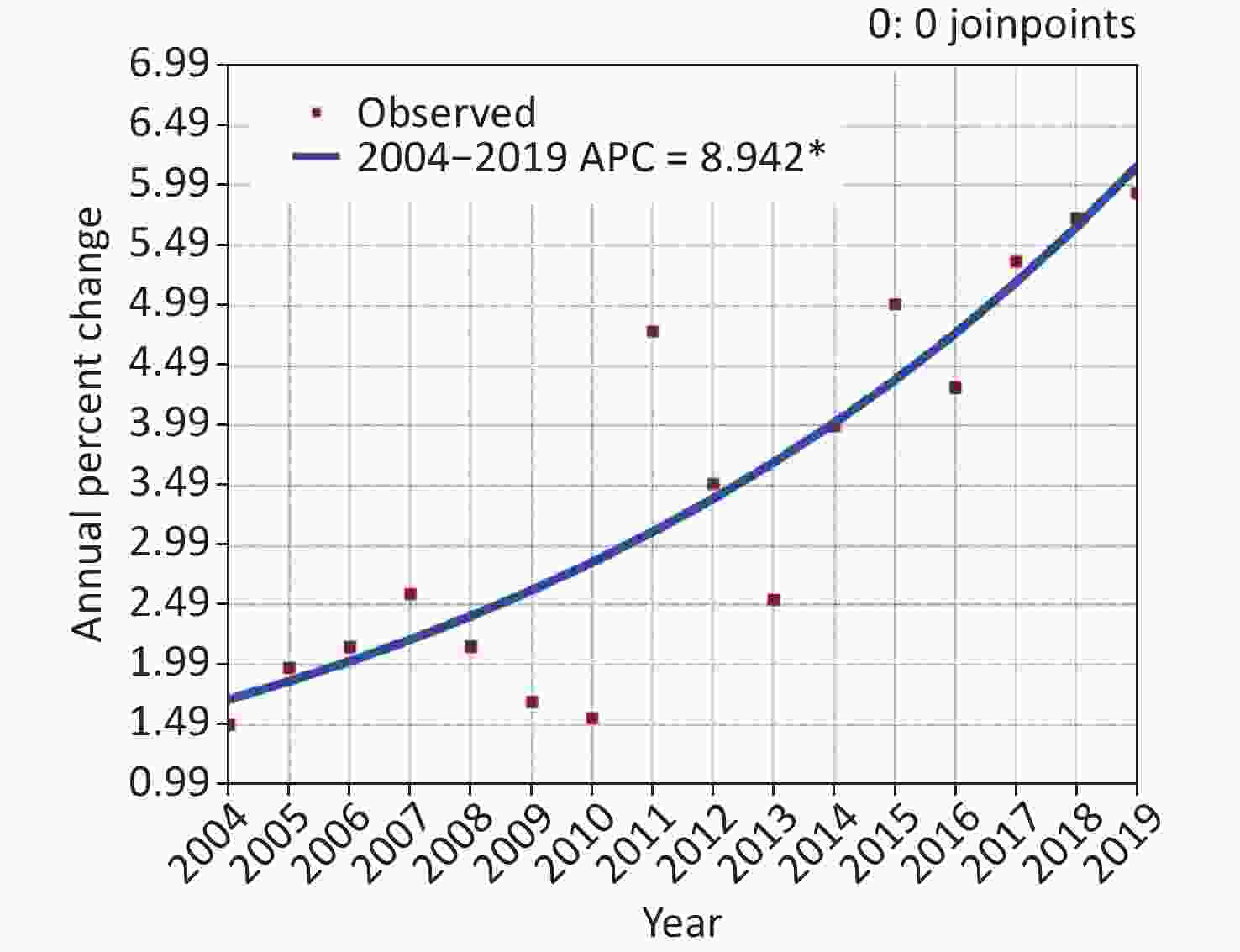
Figure S1.  Joinpoint regression showing the scarlet fever epidemic trends in the period 2004–2019. *Showed that the annual percent change (APC) is significantly different from zero at the significance level. This plot was plotted using Joinpoint regression program (Version 4.8.0.1). Joinpoint is a statistical tool for the description and analysis of trends with the Joinpoint methods. This Joinpoint Regression Program is designed as a Windows-based statistical software package to analyze Joinpoint methods. Users can use this software to investigate whether there is a statistically notable change in trend (Available from https://surveillance.cancer.gov/joinpoint/. Accessed on 16 May 2022).

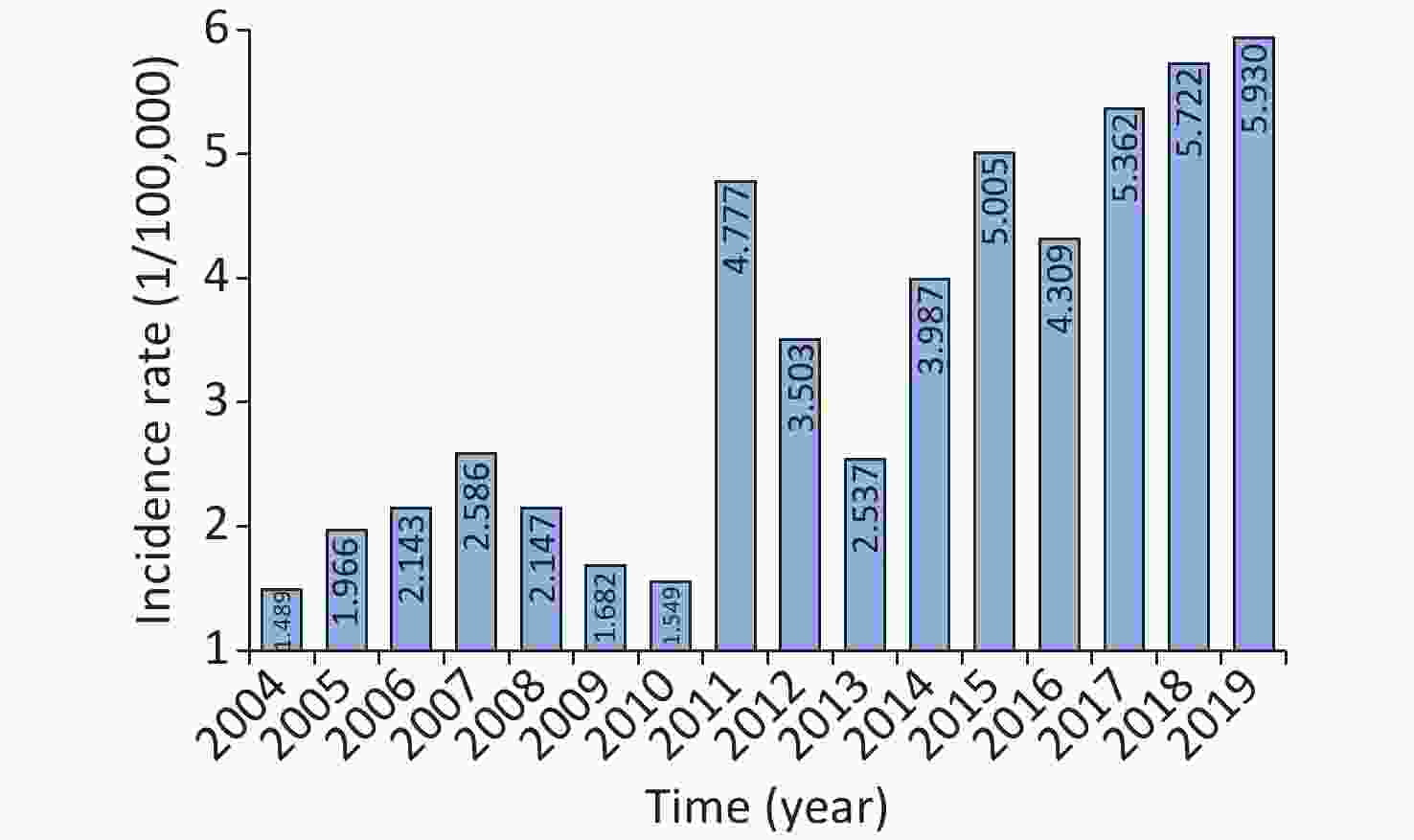
Figure S2.  The yearly incidence of SF from 2004 to 2019. It was seen that SF had the lowest incidence in 2004 (1.489 per 100,000 population) and the highest morbidity in 2019 (5.930 per 100,000 persons).

A marked semi-annual seasonal behavior occurred in the monthly SF incidence, with a strong peak between May and June, and a weak peak between November and December (Supplementary Figures S3–S4, available in www.besjournal.com). We surmised that different climatic features and beginning of spring and autumn semesters contributed to this difference in the margin of peak activities. Our seasonal profile correlates well with previous findings from Hong Kong, China ^[7]; however, discordant with that in England, which peaked between February and March ^[8]. This inconsistency may be due to the different school breaks, population density, and different GAS emm gene types in east Asia and Europe ^{[1, 8]}. In addition, the SF epidemics retain the lowest level in February every year (Supplementary Figure S3), attributable to the winter holidays and the Spring Festival.

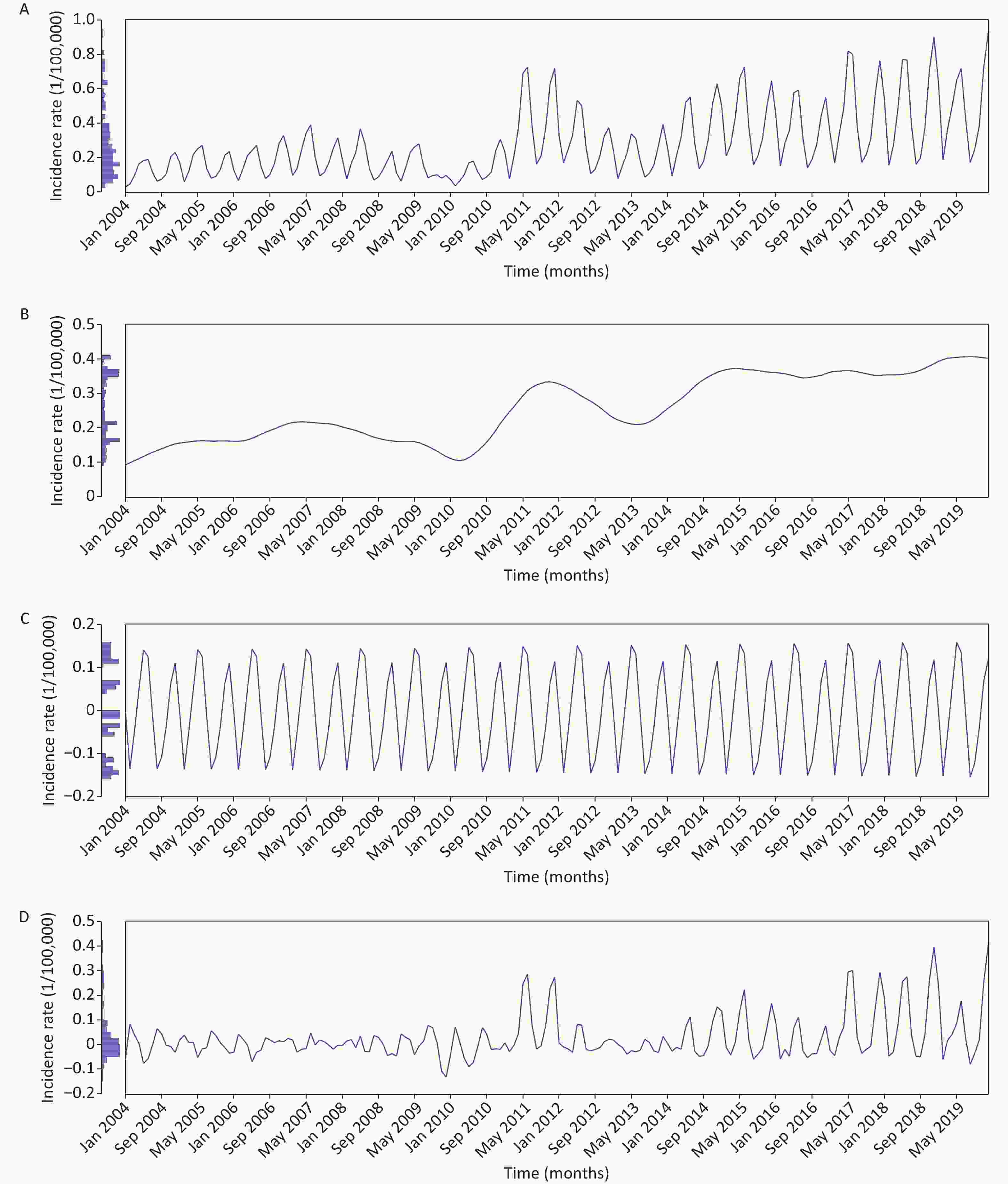
Figure S3.  Time series plot showing the monthly SF incidence rate and the decomposed seasonal, trend, and irregular components based on the STL technique. (A) Original monthly SF morbidity series. (B) Decomposed trend component. (C) Decomposed seasonal component. (D) Decomposed random component. As illustrated, overall the SF morbidity showed a rising tendency, with a sudden increase in 2011, and having notable seasonal patterns.

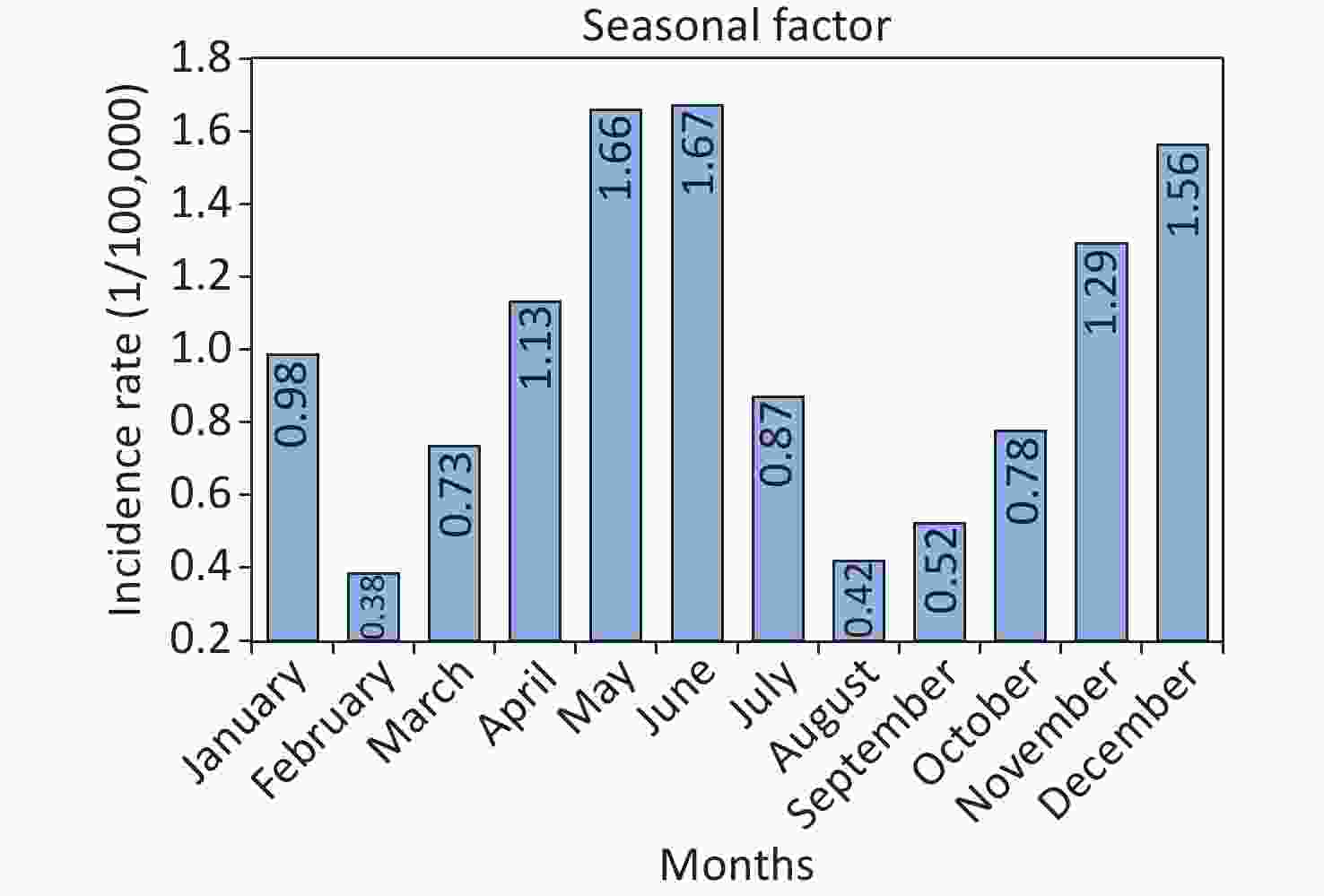
Figure S4.  The decomposed seasonal factors for the scarlet fever morbidity series using the multiplicative decomposition method (The classical Seasonal Decomposition technique can be applied to decompose a time series into a seasonal pattern, a trend component, and a random fluctuation component. This technique is implemented based on the ratio-to-moving-average method. The Seasonal Decomposition technique can be divided into two types including a multiplicative and an additive method. For a multiplicative decomposition method, the seasonal component is a factor by which the seasonally adjusted series is multiplied to produce original observed values. For a time series without seasonal variation, the seasonal pattern is deemed as one. For an additive decomposition method, the seasonal adjustments are added to the seasonally adjusted series to yield the original series. For the morbidity series of infectious diseases, the multiplicative decomposition method typically produces a more reliable decomposed result in application. By employing a multiplicative decomposition method to an object series, the seasonal pattern or seasonal factors included in the object series can be obtained. Such a decomposition is very helpful in removing the seasonal effect from a series so that we can visibly look into the other characteristics of interest in the series that may be masked by the seasonal trait^[7,8]).

The forecasts under the TBATS approach rely largely on the number of harmonics k_i applied for each seasonal pattern. As a result, in selecting the number of harmonics k_i, considering one seasonal component each time, we then fitted the model on the target data repeatedly via gradually increasing the number of harmonics k_i, but holding the remaining harmonics constant for each i until the optimal AIC is obtained. In determining the most suitable orders (p and q) of the ARMA model, we used the automatic procedure proposed by Hyndman and colleagues^[10] to fit the forecasting residuals. If the selected model with the ARMA (p, q) residual component generates a smaller AIC than the one model without the ARMA (p, q) residual component, this selected specification would be considered as the best possible model; otherwise, the ARMA (p, q) residual component is deleted. After modelling by trial and error, the TBATS (0.04, {4,0}, 0.882, {<12,5>}) specification was selected as the optimal model in that the minimum AIC (−197.965) was detected in this model, and the identified key parameters of this best TBATS model are reported in Supplementary Table S1, available in www.besjournal.com. Additional statistical diagnoses for the forecast errors are provided in Supplementary Table S2 and Supplementary Figures S5–S6, available in www.besjournal.com. The Ljung-Box Q statistics of the forecast errors produced a Q₍₁₈₎ = 11.442 with a P-value of 0.875, indicating no serial correlations in this residual series. Moreover, the ARCH effect was largely removed because the LM₍₁₈₎ = 23.808 with a P-value of 0.302. These results confirmed the adequacy of the model specifications. Similarly, based on the modelling steps described above, the TBATS (0.01, {0,0}, 0.898, {<12,5>}) and TBATS (0.048, {0,0}, 0.902, {<12,5>}) specifications tended to be the preferred models for forecasting the 12- and 36-holdout periods (Supplementary Tables S3–S4 and Supplementary Figures S7–S10, available in www.besjournal.com).

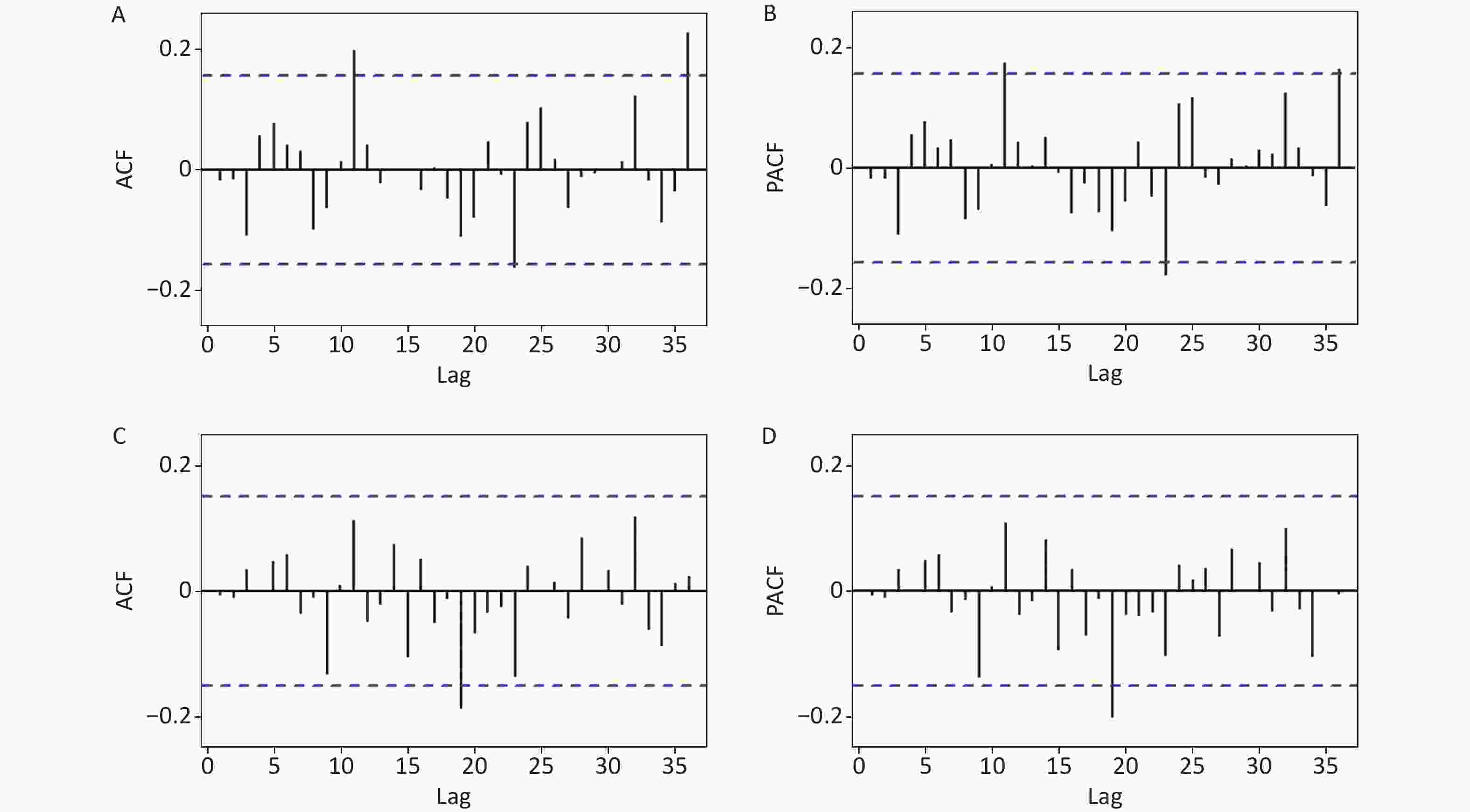
Figure S5.  Estimated autocorrelation function (ACF) and partial ACF (PACF) plots to display the statistical checking for the residual series of the SARIMA and TBATS models. (A) ACF plot for the SARIMA model. (B) PACF plot for the SARIMA model. (C) ACF plot for the TBATS model. (D) PACF plot for the TBATS model. We can see that the correlation coefficients at lags 11, 23, and 36 in Figure 2A and 2B, and at lag 19 in Figure 2C and 2D touched the confidence levels (this is reasonable as the correlation coefficients at higher-order may exceed the significance bounds by chance alone), but all other correlation coefficients at different lags failed to touch the confidence levels, seemingly suggesting effective and sufficient models.

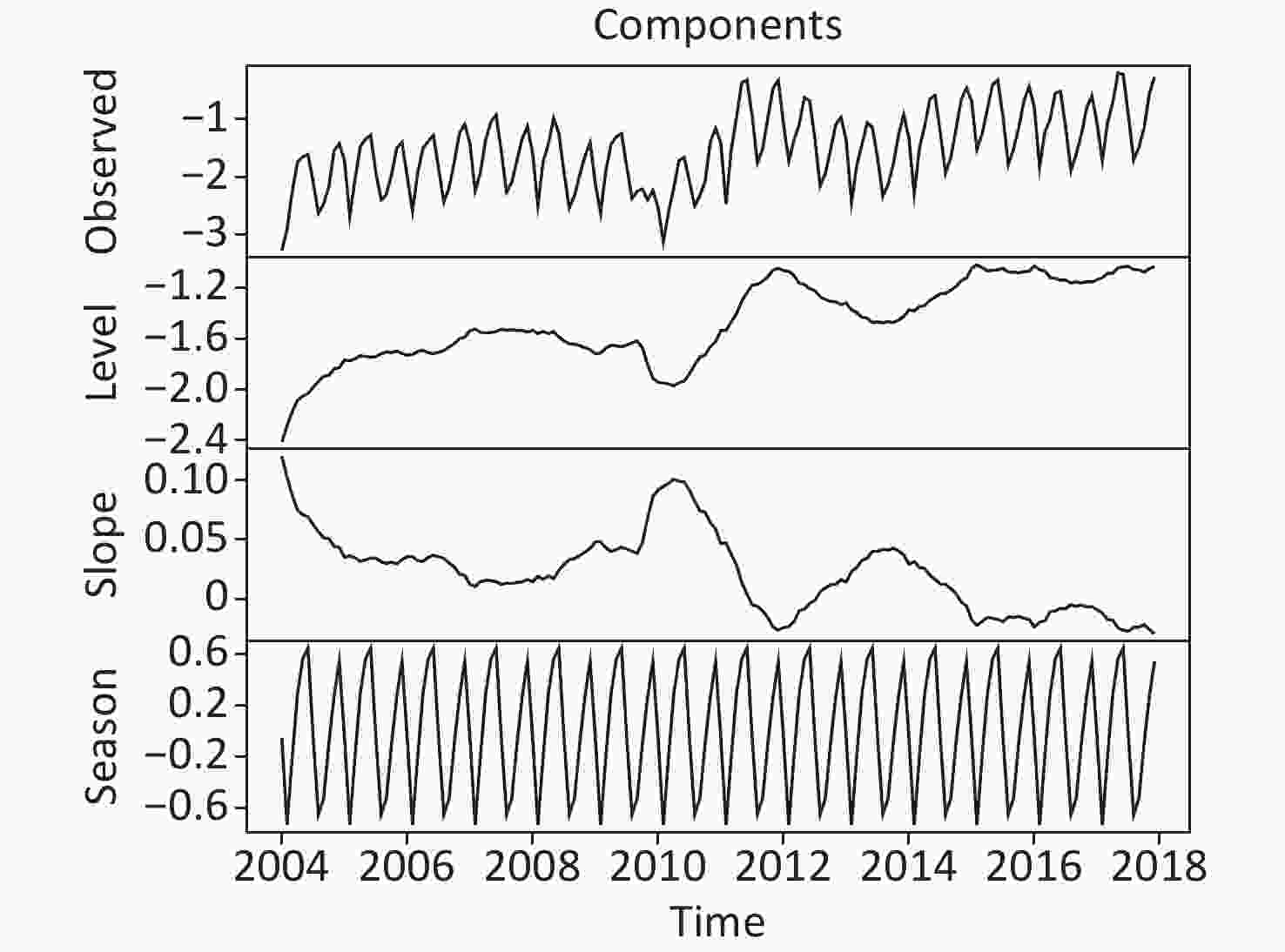
Figure S6.  The extracted level, slope, and seasonal components of the best TBATS method developed on the basis of the data from January 2004 to December 2017.

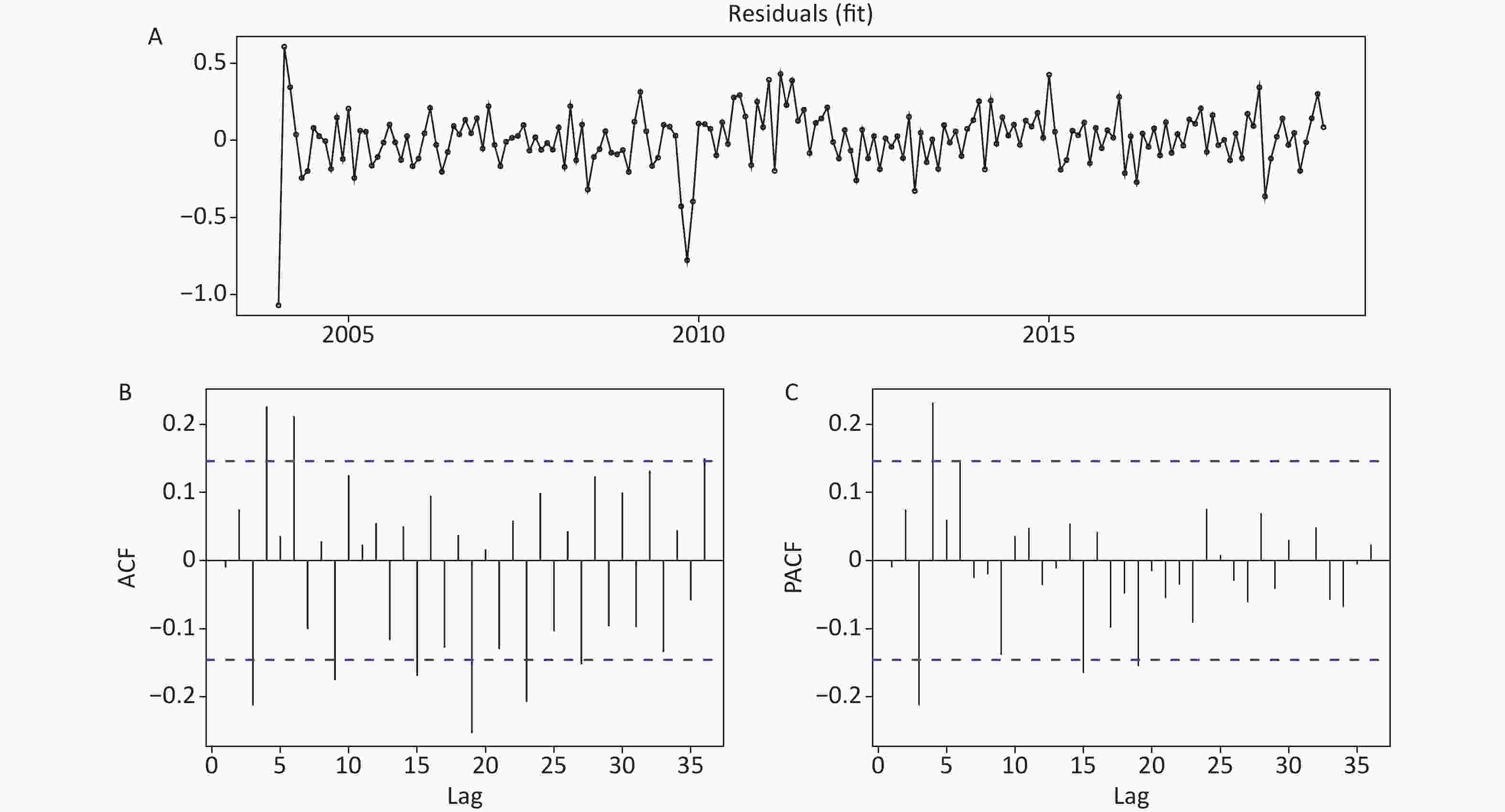
Figure S7.  Statistical checking for the residual series of the TBATS model developed on the basis of the data from January 2004 to December 2018. (A) Time series plot showing the residual series. (B) Autocorrelation function (ACF) plot. (C) Partial autocorrelation function (PACF) plot. The correlogram shows that although there are some residual ACF and PACF for the forecast errors that exceed the significance bounds, this is the best model used to estimate the upcoming 12-month epidemics of scarlet fever.

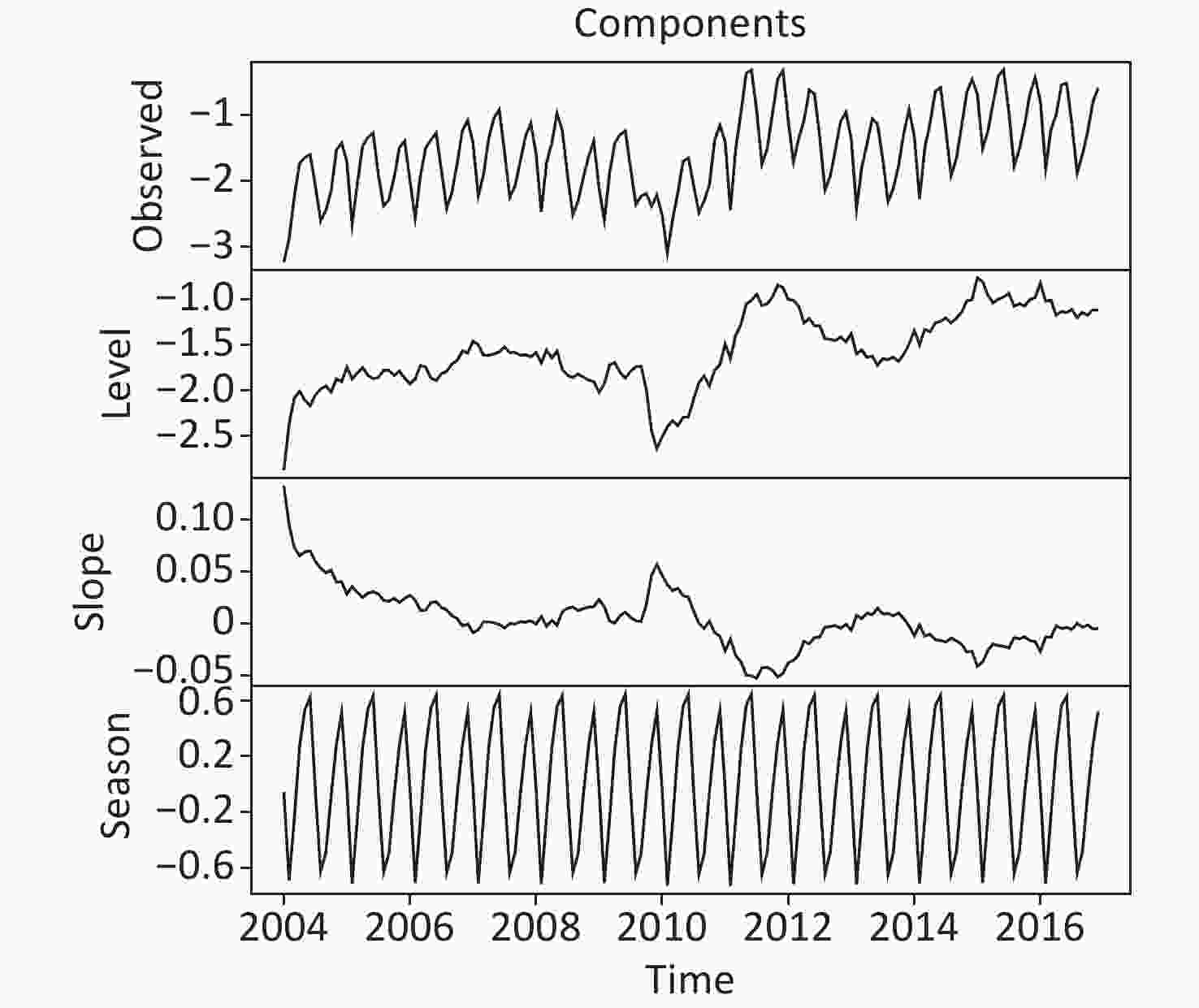
Figure S10.  The extracted level, slope, and seasonal components of the best TBATS method developed on the basis of the data from January 2004 to December 2016.

Similarly, following the SARIMA modelling steps, the optimal SARIMA models on different datasets were identified (Supplementary Tables S2–S5, and Supplementary Figures S5, S11–S12, available in www.besjournal.com). Subsequently, the best SARIMA and TBATS models could be used to perform multistep ahead predictions (Figure 1 and Supplementary Figures S13–S14, available in www.besjournal.com). Table 1 lists the measurement metrics, which indicate the forecasting reliability levels on different time windows under the preferred SARIMA and TBATS models. The optimal TBATS models provided a smaller MAD, MAPE, RMSE, RMSPE, and MER compared with the optimal SARIMA models, with a performance improvement of almost 50% in the forecasting abilities for estimating both short- and long-term epidemiological trends, albeit the predictive potential showed a slight reduction with the increase in prediction time windows. We further compared the forecasting abilities of both methods for 48- and 72-step ahead predictions, and the comparative results are listed in Supplementary Tables S1, S6–S7, and Supplementary Figures S15–S16 (available in www.besjournal.com), which show a similar finding, but the predictive results deviated from the epidemic trajectories. In addition, we used the SF incidence data in Liaoning, Heilongjiang, and Shandong provinces, and Inner Mongolia (which are the hardest hit areas by SF in China in the last decade ^{[2, 3]}) to assess the predictive quality of these two methods. Likewise, the TBATS method produced lower error rates in all the datasets (Supplementary Table S8, available in www.besjournal.com). Our recent study indicated that the Error-Trend-Seasonal (ETS) model also has a powerful potential in estimating the long-term epidemic behaviors of diseases ^[4]. As a result, we further developed the ETS model based on the SF morbidity to predict the epidemiological trends, and the results also showed similar findings (the computed MAPE values were 16.101% vs. 38.511%, 21.142% vs. 28.273%, and 23.984% vs. 26.735% in the 12-, 24-, and 36-step ahead forecasts, respectively; Supplementary Table S9, available in www.besjournal.com). These findings further substantiated the utility of the TBATS model. The TBATS model was introduced by adding the trigonometric representation of seasonal components based on the Fourier series into the traditional BATS model, which enabled handling of all complex time series, as well as linear and non-linear information ^[5], thus indicating the suitability and adequacy of this model. Considering the attractive advantages of the TBATS model, this model can be recommended as a flexible and useful long-term predictive tool in assessing the epidemic patterns of SF in other countries or other contagious diseases; however, further work is required for validation. Moreover, with the rapid advances in the forecasting domain of time series, many hybrid prediction models (e.g., SARIMA-BPNN, SARIMA-GRNN, and SARIMA-LSTM) have also been reported to show an attractive advantage in estimating the long-term epidemic trajectories of diseases. Therefore, what is now needed are studies involving comparisons of the predictive reliable level between the TBATS model and the above-mentioned models.

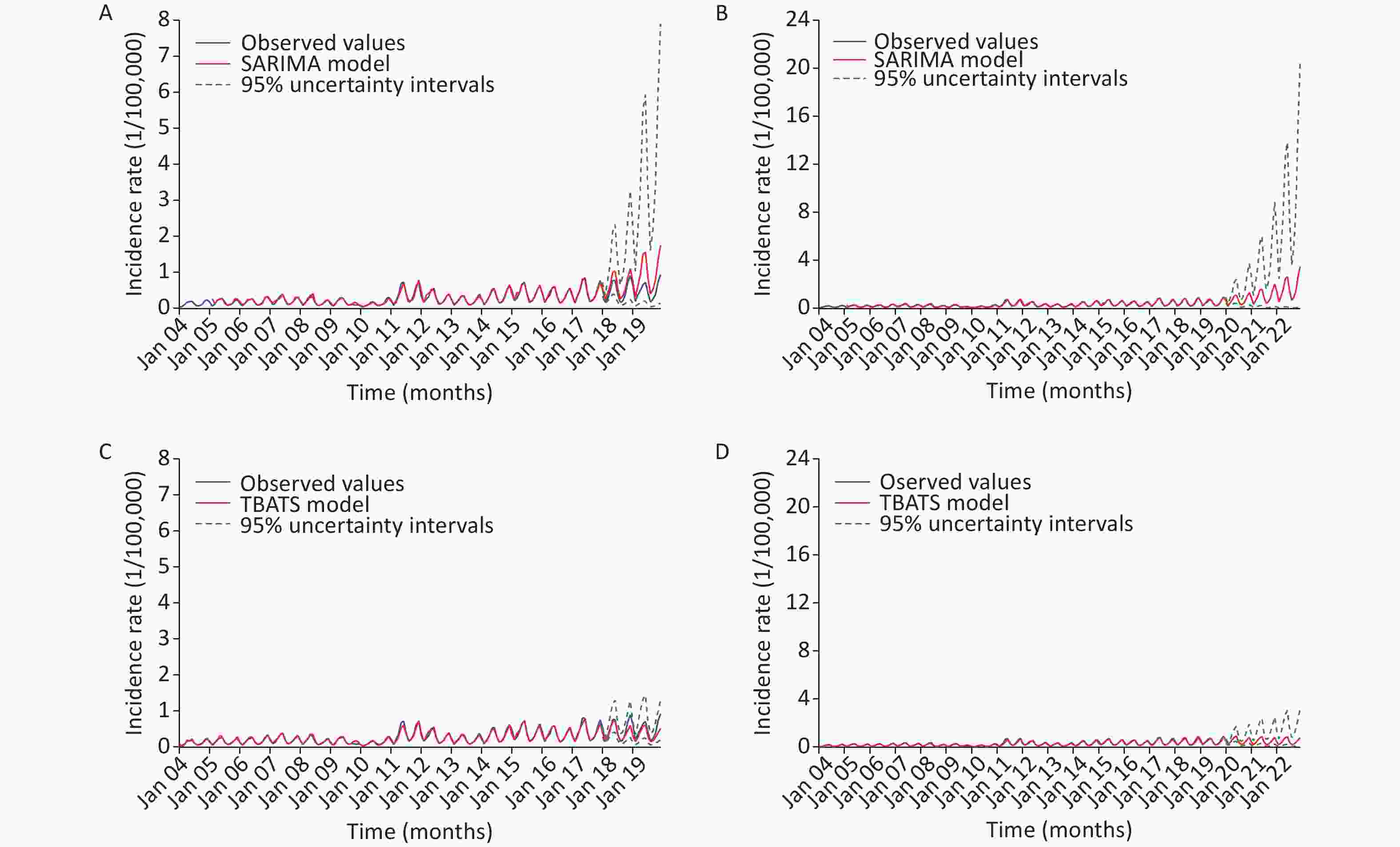
Figure 1.  Comparative results of the forecasts based on the SARIMA and TBATS models. (A) The comparison between the 24-step ahead forecasts of the SARIMA model and the observed values. (B) The predicted upcoming 36-month values from January 2020 to December 2022 using the SARIMA model. (C) The comparison between the 24-step ahead forecasts of the TBATS model and the observed values. (D) The predicted upcoming 36-month values from January 2020 to December 2022 using the TBATS model.

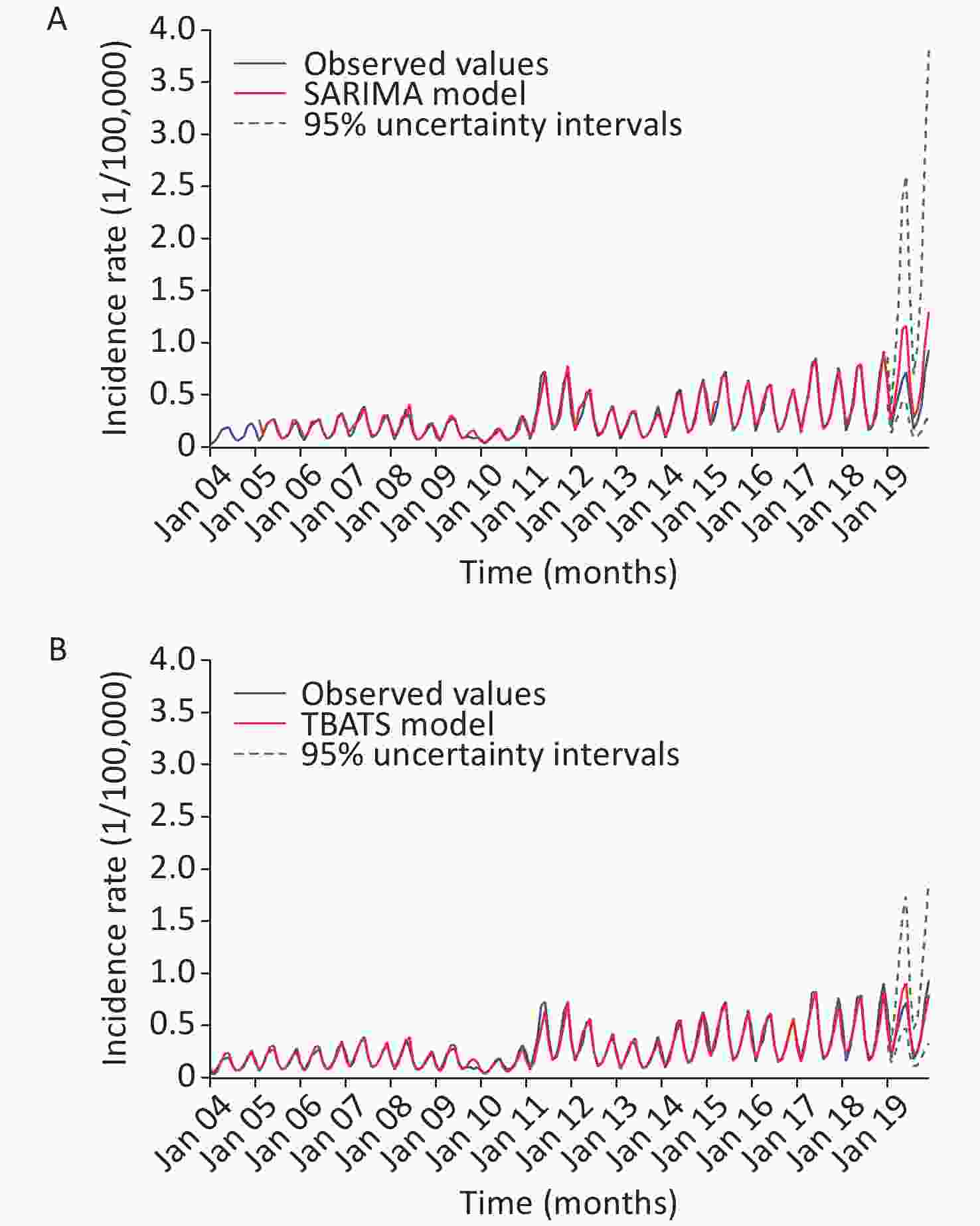
Figure S13.  Comparative results of the forecasts based on the SARIMA and TBATS models. (A) The comparison between the 12-step ahead forecasts of the SARIMA model and the observed values. (B) The comparison between the 12-step ahead forecasts of the TBATS model and the observed values.

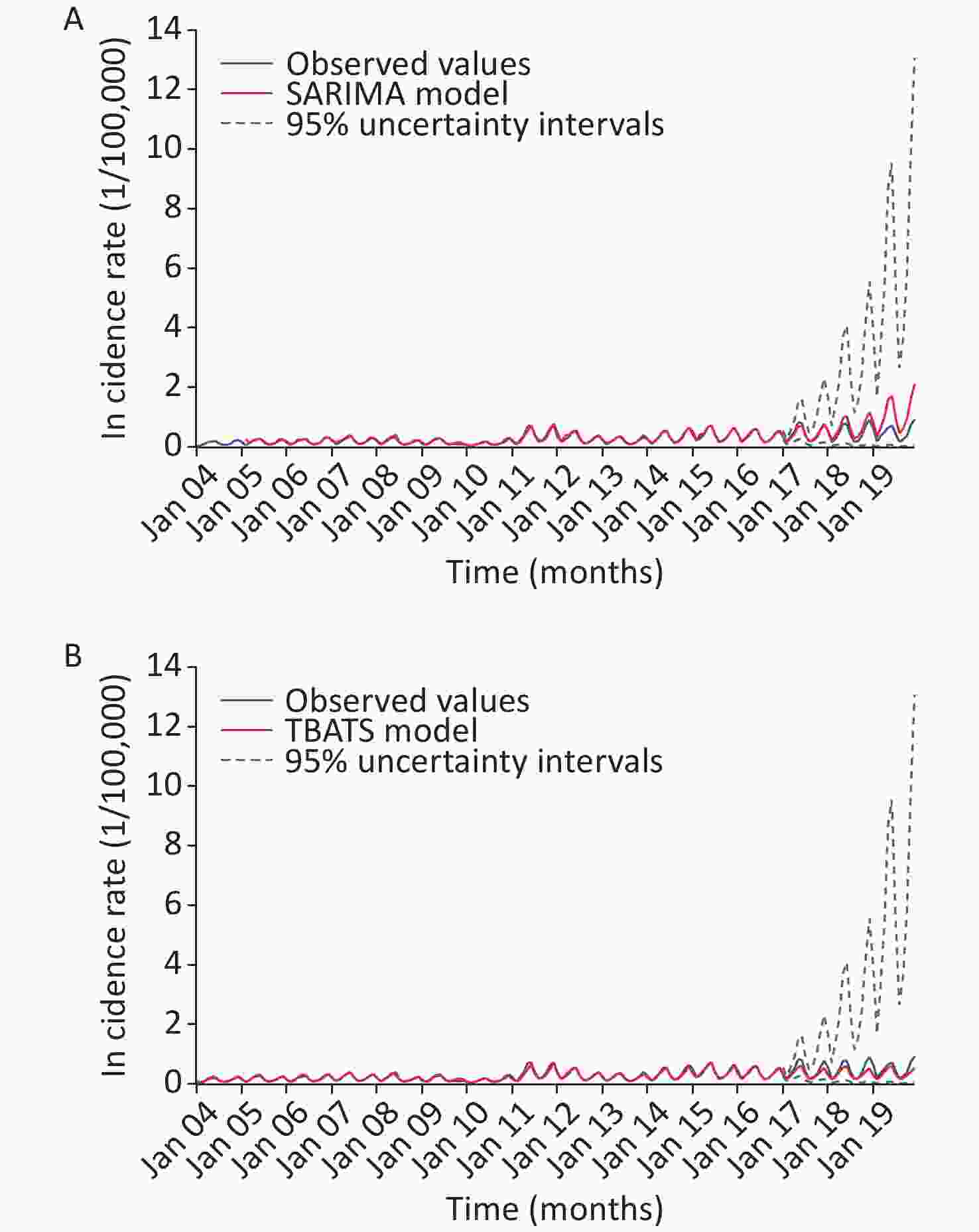
Figure S14.  Comparative results of the forecasts based on the SARIMA and TBATS models. (A) The comparison between the 36-step ahead forecasts of the SARIMA model and the observed values. (B) The comparison between the 36-step ahead forecasts of the TBATS model and the observed values.

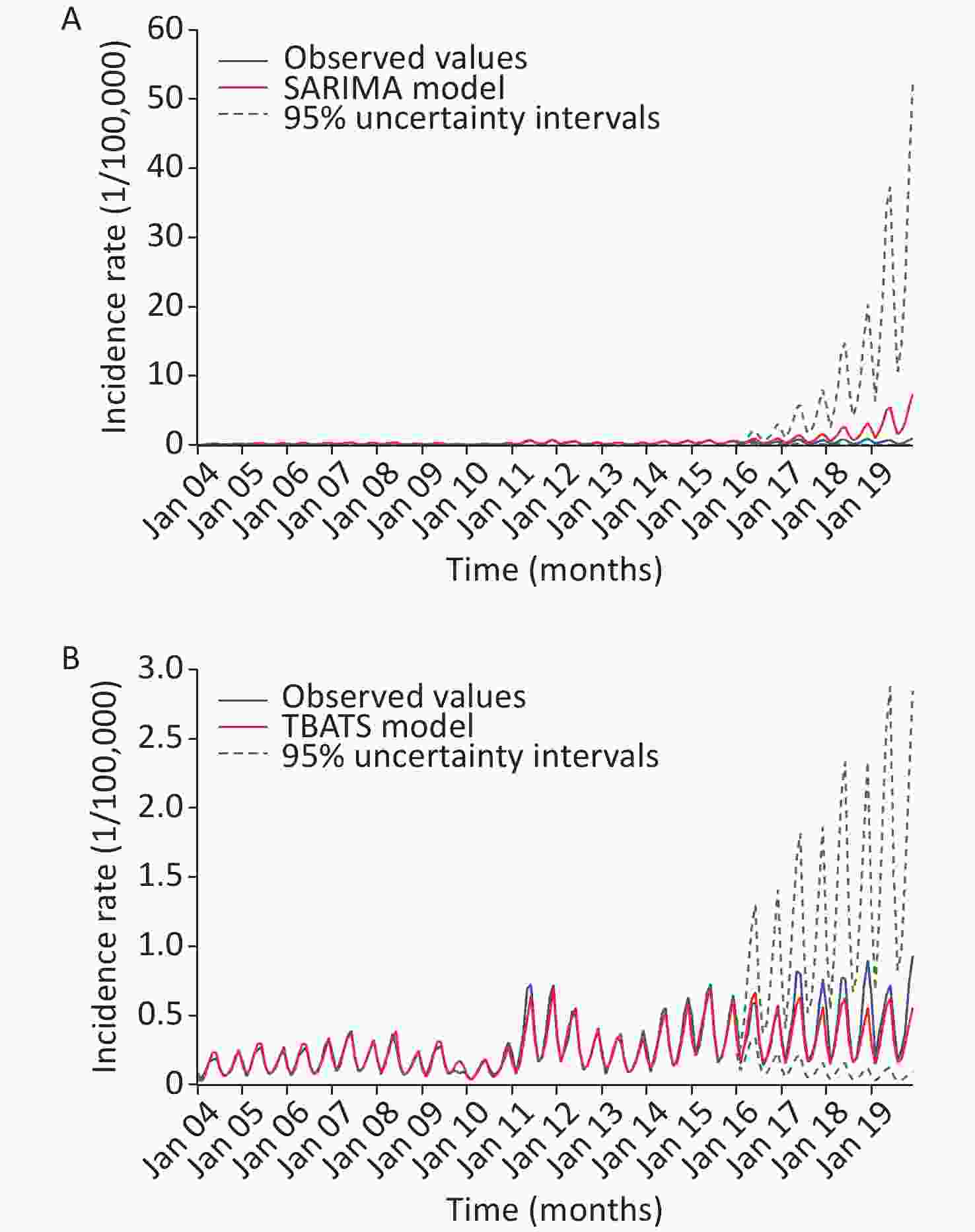
Figure S15.  Comparative results of the forecasts based on the SARIMA and TBATS models. (A) The comparison between the 48-step ahead forecasts of the SARIMA model and the observed values. (B) The comparison between the 48-step ahead forecasts of the TBATS model and the observed values.

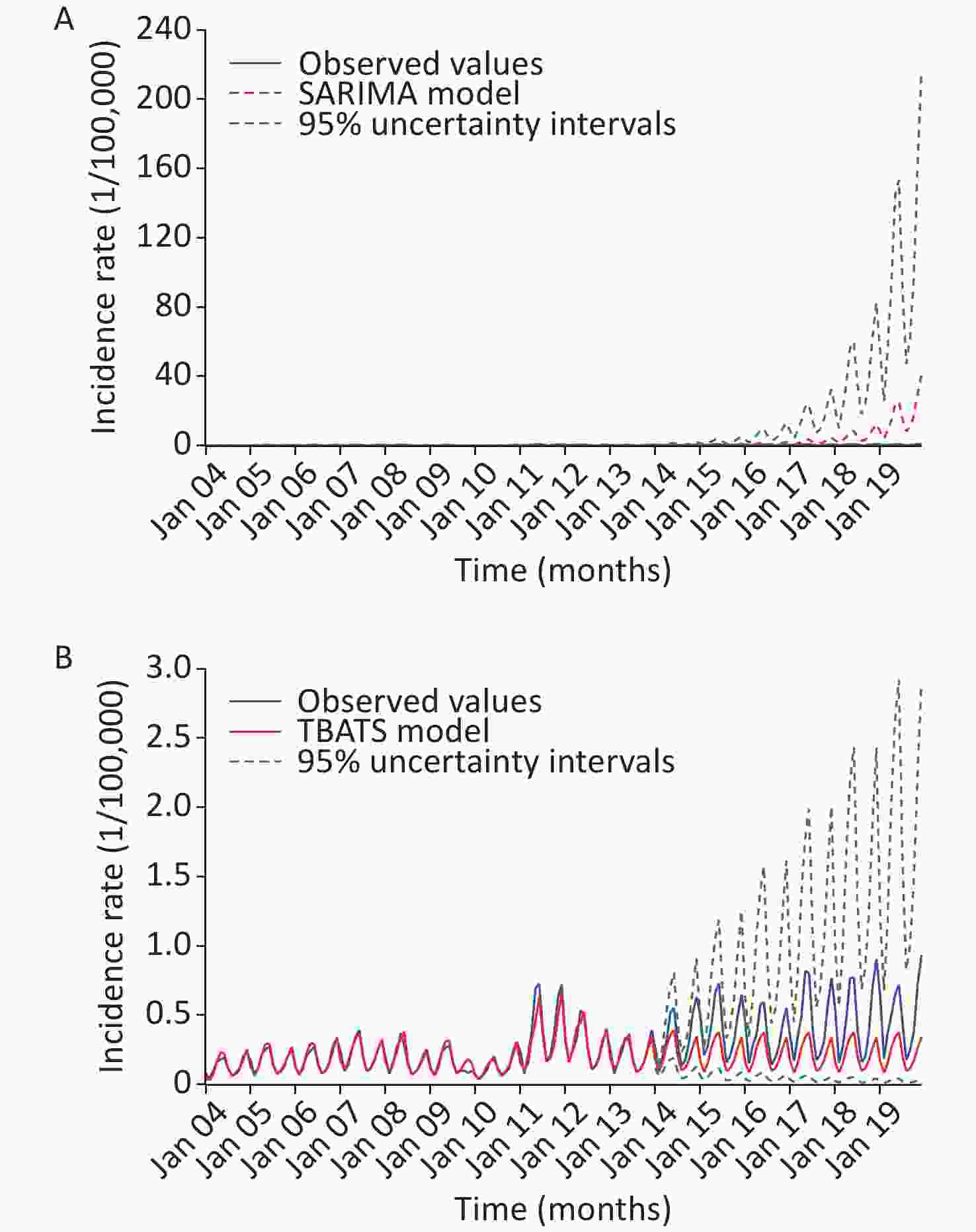
Figure S16.  Comparative results of the forecasts based on the SARIMA and TBATS models. (A) The comparison between the 72-step ahead forecasts of the SARIMA model and the observed values. (B) The comparison between the 72-step ahead forecasts of the TBATS model and the observed values.

This study had some limitations. First, SF is a mild illness and has rarely led to death since the 20^th century ^[3]. Therefore, infected individuals with mild clinical manifestations sometimes fail to seek medical aid, resulting in under-reporting and under-diagnosis. Second, to ensure that the model obtained a satisfactory forecasting result, it is important to note that this model should be updated with new incidence data. Third, to investigate whether our TBATS model was adequate for estimating the SF epidemics in other study regions or other infectious diseases, much work is still needed. Finally, integrating the factors influencing the SF epidemics may improve the predictive power. Nevertheless, we are not able to perform such an analysis due to the unavailability of a multivariate TBATS method and SF-related factors.

In summary, SF had dual seasonal behaviors, peaking in May–June and November–December, with a recurrence in 2011 in China; since then it started to be increasing in the SF incidence. The TBATS method was advantageous in analyzing the long-term epidemiological seasonality and trends of SF, which can be considered a useful and flexible alternative to aid stakeholders to develop practical solutions to stop the ongoing spread of SF in China. In addition, we re-established the preferred TBATS (0.023, {0,0}, 0.895, {<12,5>}) specification based on the 16 years of data to predict the SF incidence into 2022, although the SF incidence was predicted to reach a plateau in the next 3 years [Supplementary Tables S1 and S10 (available in www.besjournal.com), and Figure 1], the SF incidence remained at a high level, suggesting that additional or comprehensive interventions must be developed to manage this evolving scenario.

Data Availability　All the data supporting the findings of the work are contained within the Supplementary Material (Supplementary Table S11, available in www.besjournal.com).

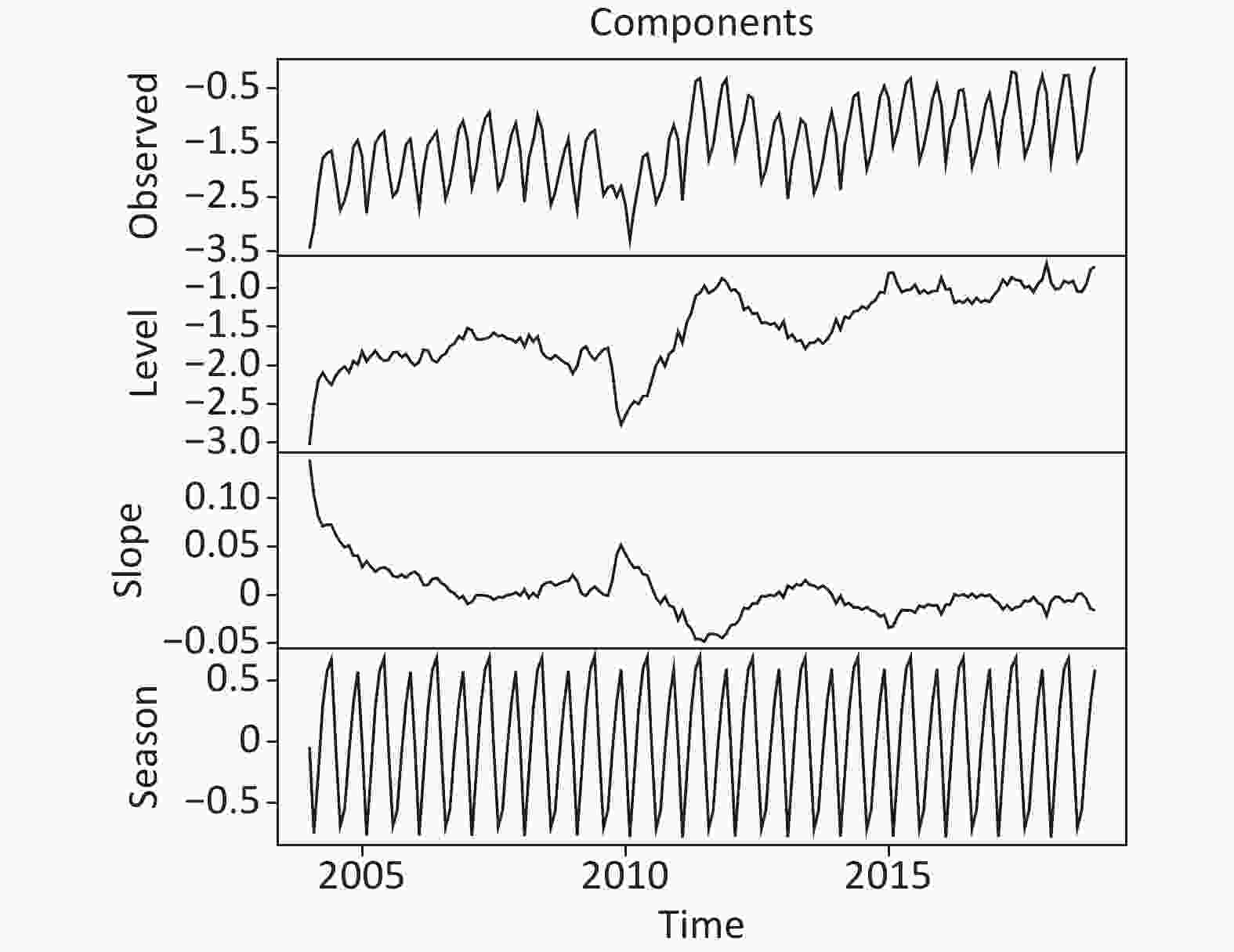
Figure S8.  The extracted level, slope, and seasonal components of the best TBATS method developed on the basis of the data from January 2004 to December 2018.

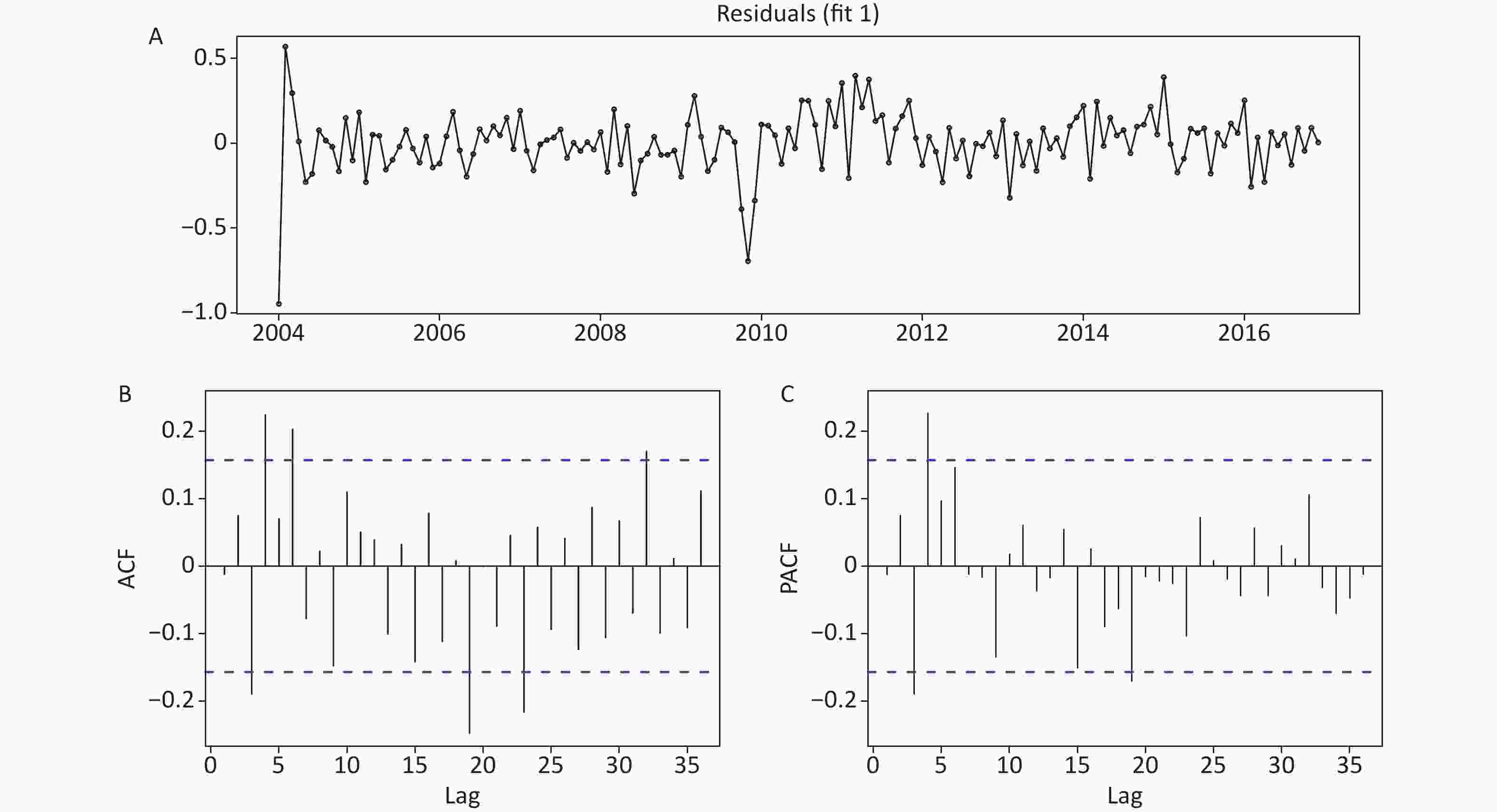
Figure S9.  Statistical checking for the residual series of the TBATS model developed on the basis of the data from January 2004 to December 2016. (A) Time series plot showing the residual series. (B) Autocorrelation function (ACF) plot. (C) Partial autocorrelation function (PACF) plot. The correlogram shows that although there are some residual ACF and PACF for the forecast errors that exceed the significance bounds, this is the best model used to estimate the upcoming 36-month epidemics of scarlet fever.

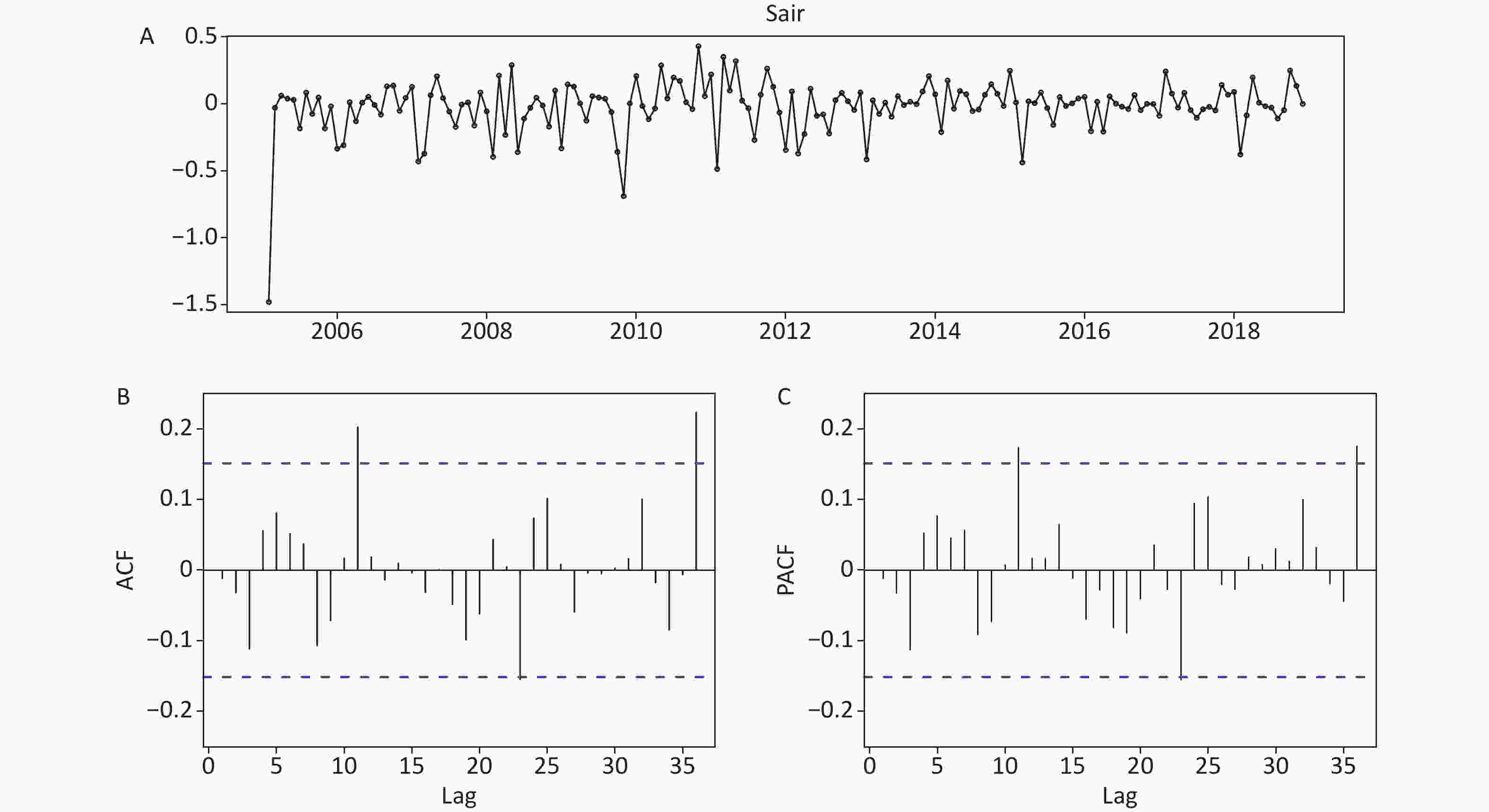
Figure S11.  Statistical checking for the residual series of the SSARIMA model developed on the basis of the data from January 2004 to December 2018. (A) Time series plot showing the residual series. (B) Autocorrelation function (ACF) plot. (C) Partial autocorrelation function (PACF) plot. The correlogram shows that the ACF and PACF for the forecast errors do not exceed the significance bounds except for lags 11, 23, and 36, indicating that there is little evidence of non-zero autocorrelations at lags 1–36.

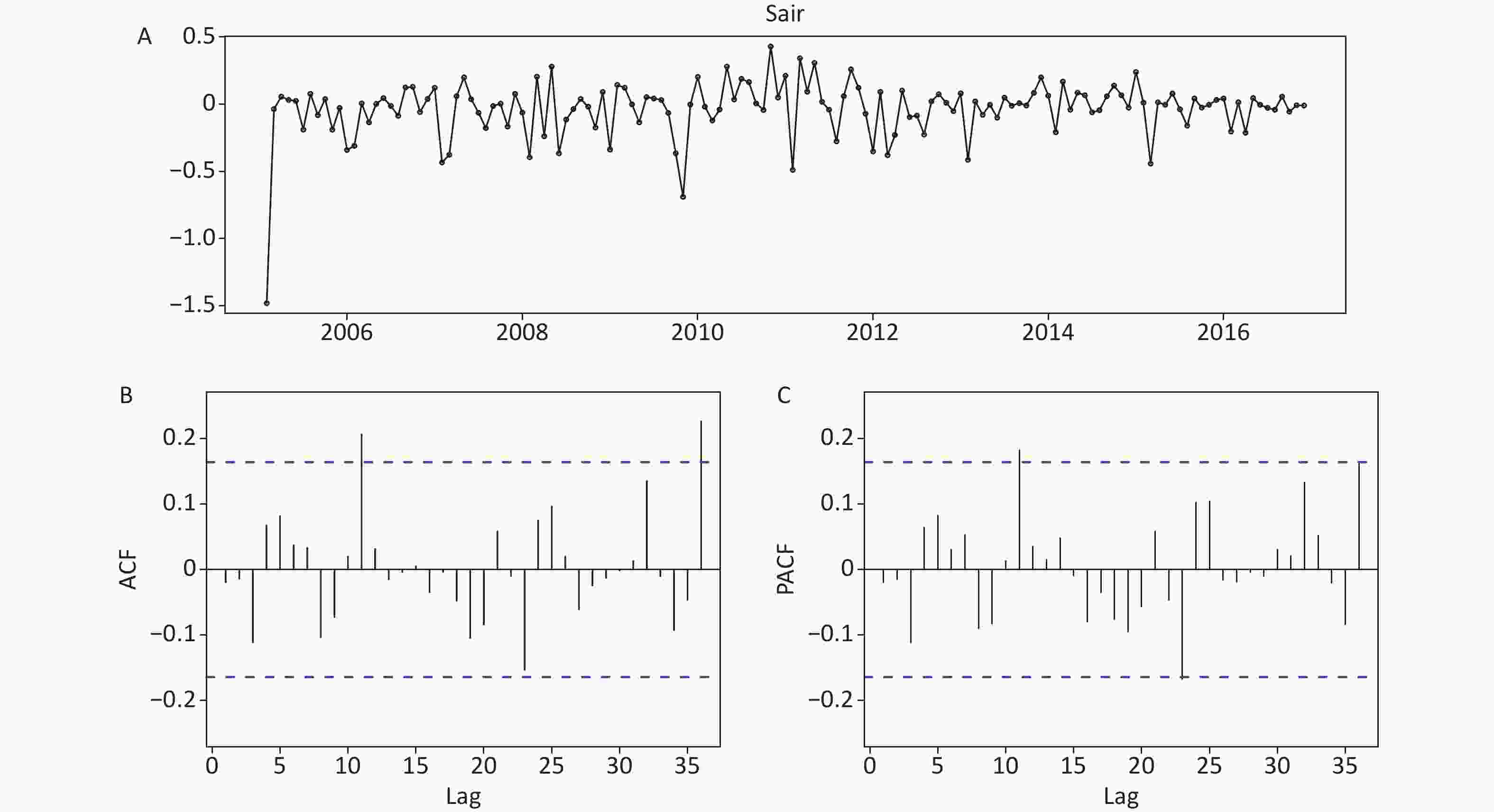
Figure S12.  Statistical checking for the residual series of the SARIMA model developed on the basis of the data from January 2004 to December 2016. (A) Time series plot showing the residual series. (B) Autocorrelation function (ACF) plot. (C) Partial autocorrelation function (PACF) plot. The correlogram shows that the ACF and PACF for the forecast errors do not exceed the significance bounds except for lags 11 and 36, indicating that there is little evidence of non-zero autocorrelations at lags 1–36.